ニューラルネットワークで使用される各層の回帰・分類の分析は、誤った認識のデータを以下に取り入れないようにして分析するかが重要になってきます。ノイズ対策を目的とした回帰と分類の分析手法は様々なものがありますが、代表的な方法を紹介します。
まずは回帰分析において使用される「ベイズ線形回帰」「サポートベクター回帰」「ランダムフォレスト」の手法を紹介します。
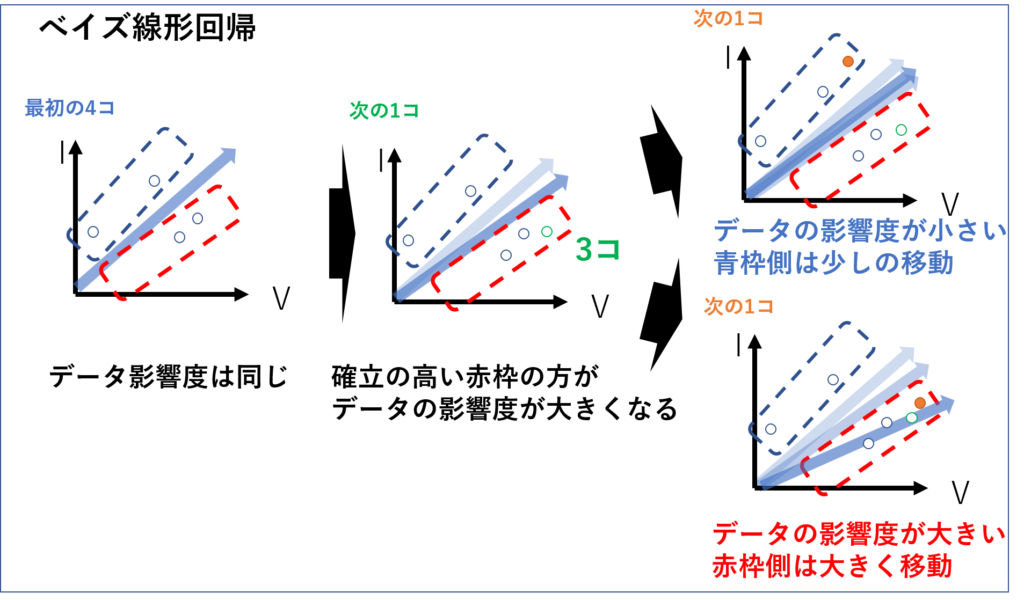
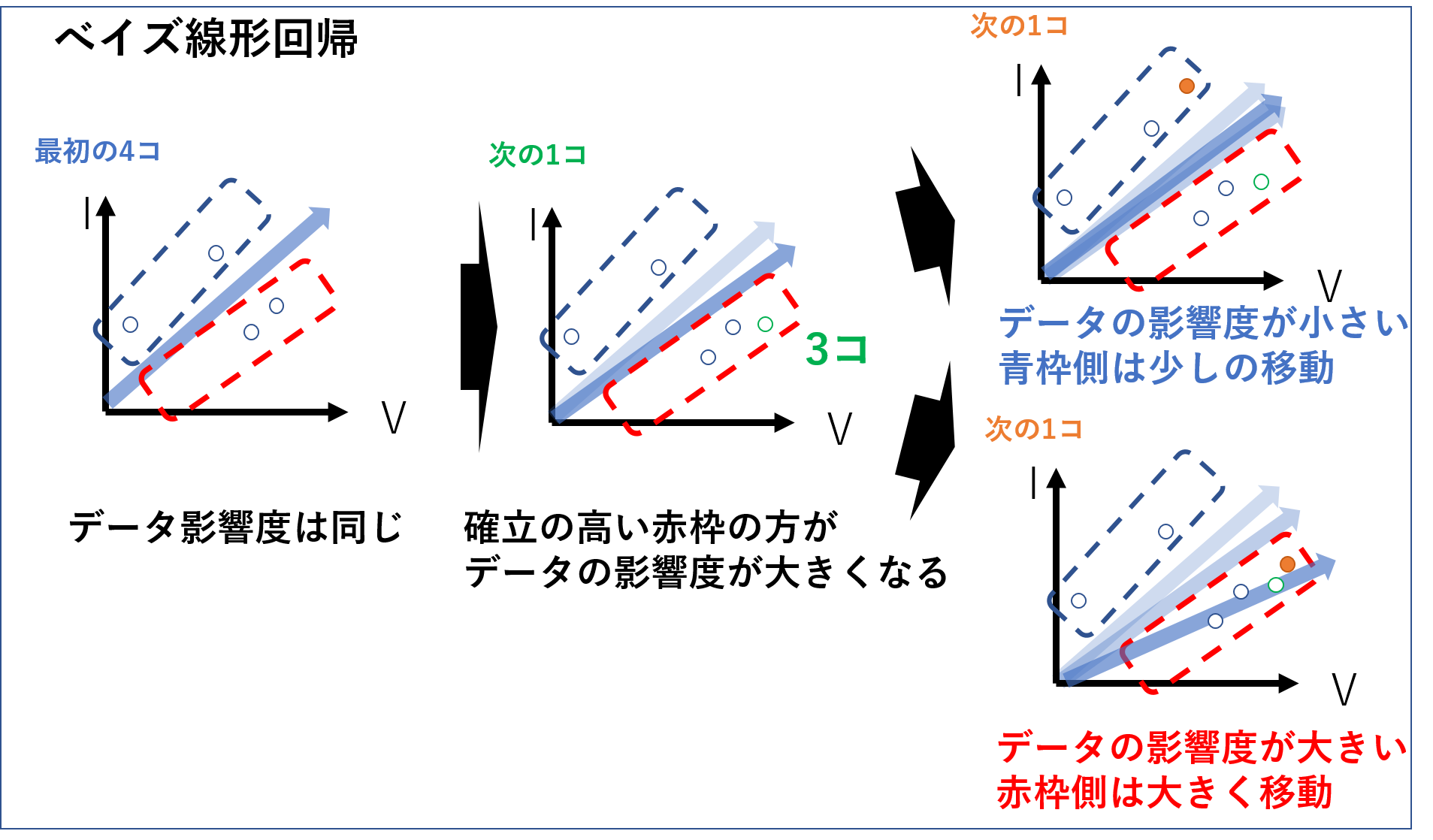
「ベイズ線形回帰」は、繰り返し蓄積されてゆくデータの分布度合いに応じて次に新しく来るデータの分布確立を計算し、確立の大きい方に次のデータが来たとき、回帰分析が受ける影響度を大きくする手法です。上記のようにデータが読み込まれたとき、最初の４コのデータでは赤青両方の範囲とも2：2の割合でデータが入り次に来る確率は1/2なわけですが、次のデータで赤枠に1コのデータが入ると青枠より赤枠に入る確率が上がります。そうしたとき、高い確率の赤枠にデータが入ると回帰分析の影響を大きく、低い確率の青枠にデータが入ると回帰分析の影響を小さくしておくことで、次の1コのデータがたとえ青枠(ノイズ)であったとしても、悪影響を減少させて早く精度の良い回帰分析値へ到達させる方法です。
「サポートベクター回帰」は、回帰分析の線の周辺にプロットされたデータのみ認識し、赤塗の範囲から外れたデータを認識させないようにすることで、ノイズデータを拾わないように回帰分析を行う方法です。
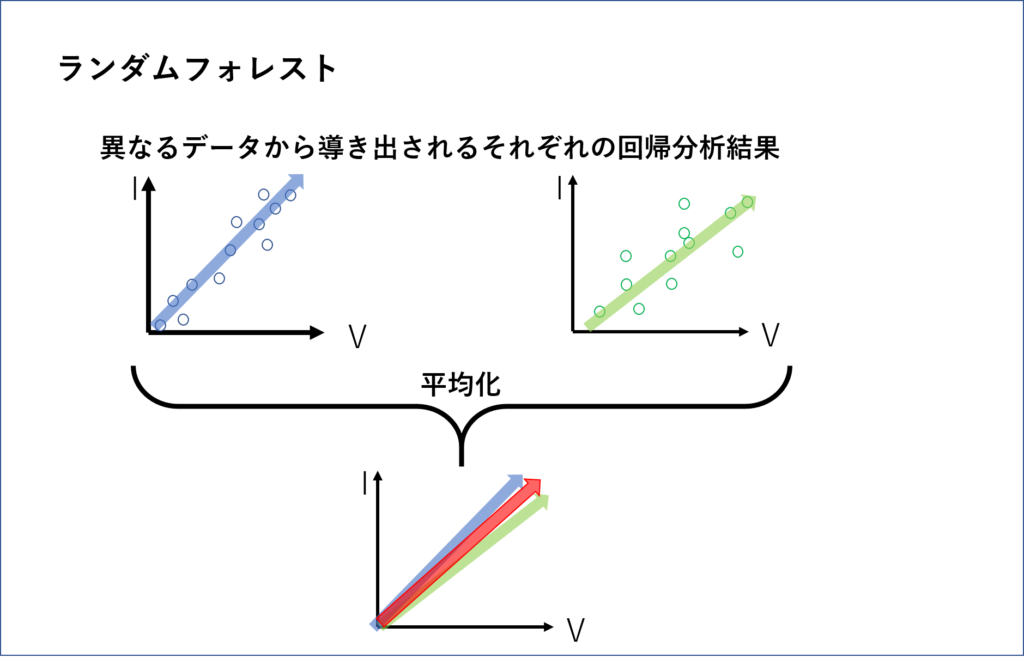
「ランダムフォレスト」は、教師データをランダムにいくつかに分けて、同じ回帰分析を行わせ、最後にその結果を平均化させて回帰分析の線とすることで、精度を上げる方法です。
続いて、分類分析で用いられる「ｋ近傍法」と「ロジスティック回帰」を紹介します。
「k近傍法」は、分類対象のデータを、その周辺に位置する教師データのプロットの数の多い方で判別する、多数決方式の判別方法です。
「ロジスティック回帰」は、入力パラメータごとの教師データの分布からロジスティック関数といわれる数式に近似することで、確立として分類する手法です。第二回の分類を用いた説明でも使用ています。
コメント