ディープラーニングの仕組みってどうなっているの？３回目（教師あり学習：勾配降下法と誤差逆伝搬法） /学習過程からわかるディープラーニングの仕組み / もしも目指すなら

1回目と２回目は、①答え(教師データ)を決めて行う学習の仕組みについて取り上げました。３回目では、学習を行って正しい回答予測にたどり着くまでのプロセス（アルゴリズム）について説明します。

以下のように、入力されるデータX₁とX₂の入力データの横軸の順番を同じ順番に並べて、ニューロンの計算の流れをグラフで考えます。

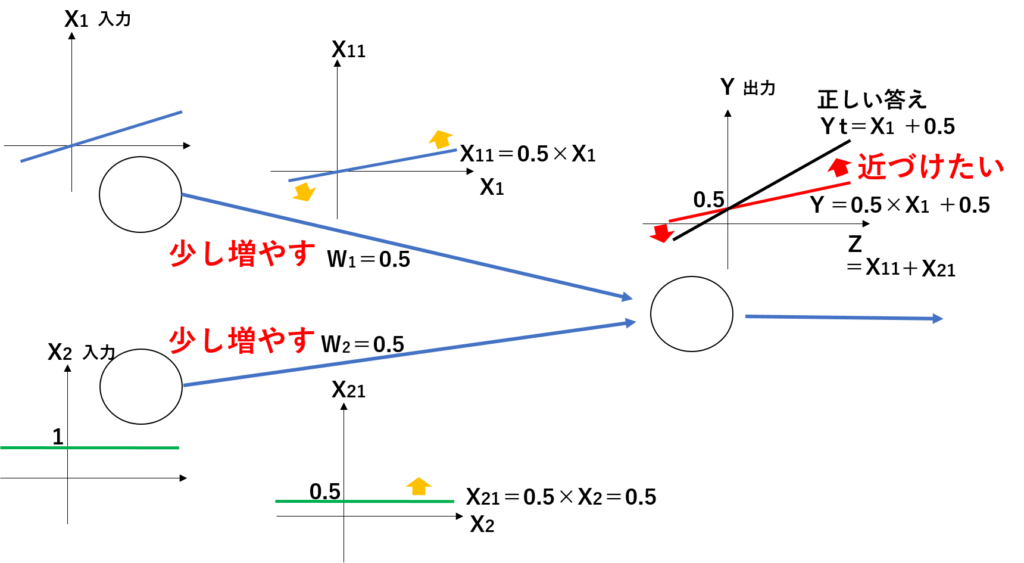
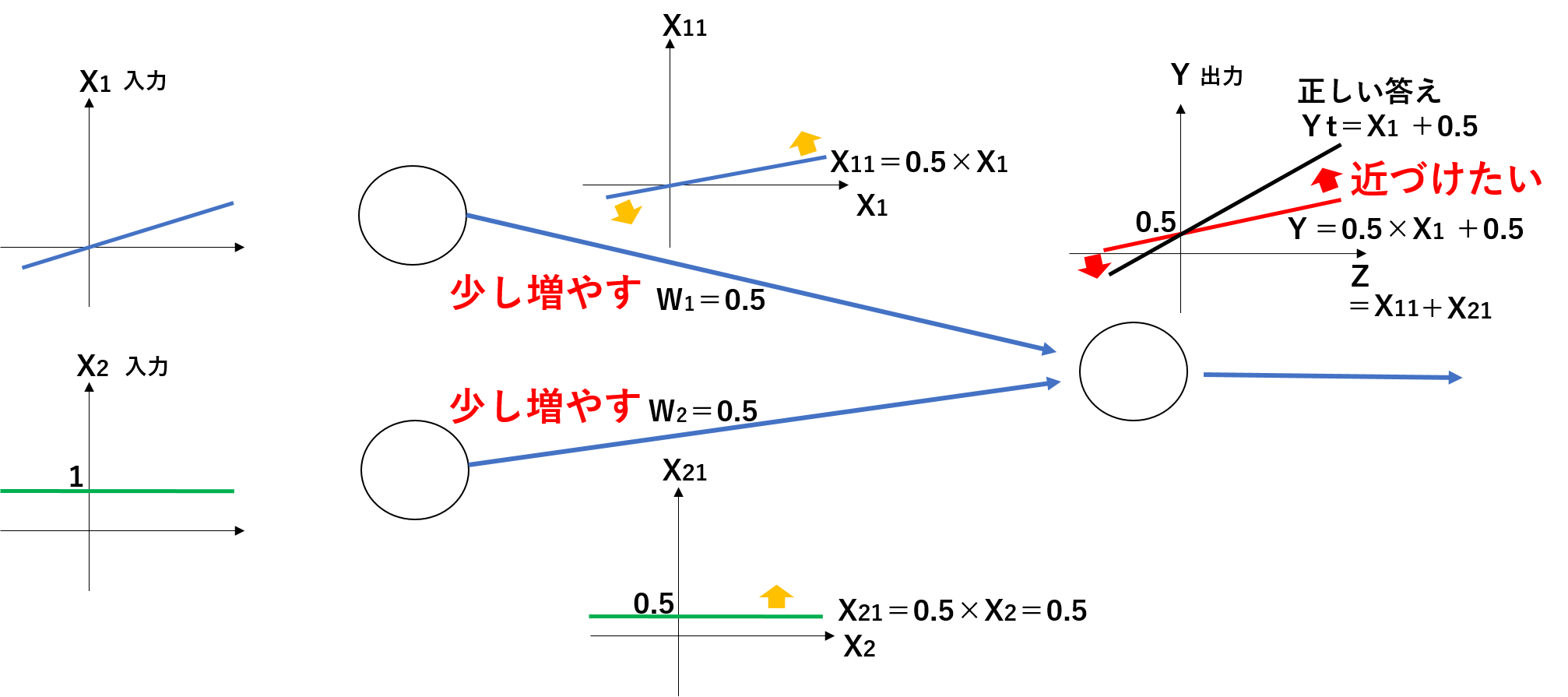
X_１とX_２の６回分の入力データが学習用に読み込まれたとき、それぞれのデータに重みW₁とW₂をそれぞれ掛けた結果X₁₁とX₂₁が合わさって、たし合わせることで、Yが出力されます。

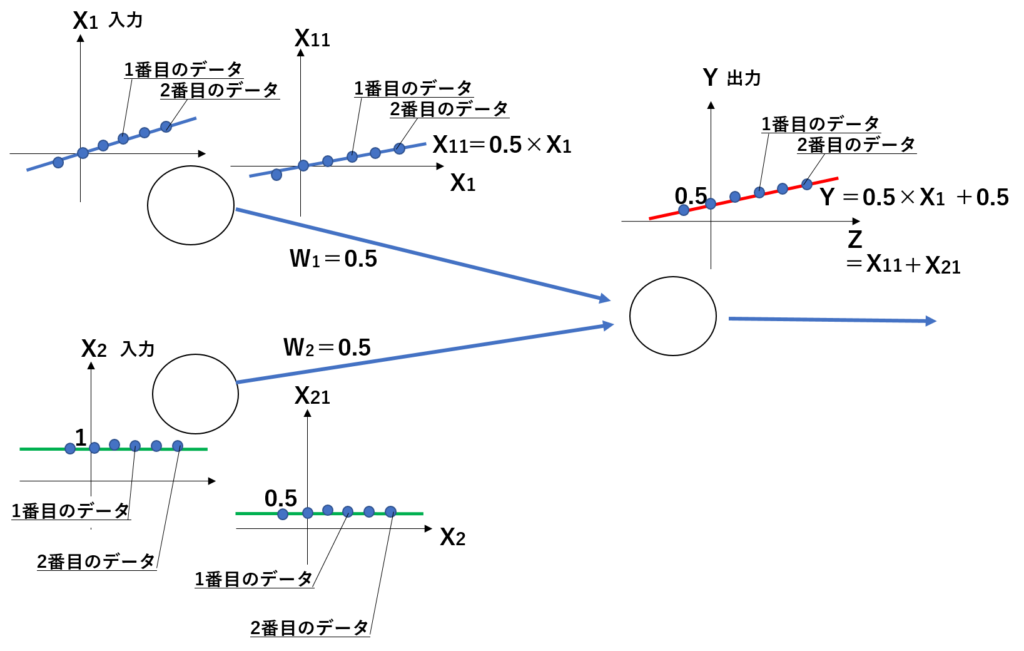
この時、出力されたYの結果のグラフが、正しい答えのグラフYtと違ったとします。人が見るとグラフからW₁だけ変化させて傾きを変えてあげればよいと判断ができますが、ニューラルネットワークによる学習ではそれができません。出力されたYのグラフを正しい答えのグラフYtに向けて、少しづつ重さW₁とW₂の両方を変化させて答えにたどり着かせる仕組みとなります。この時、誤差を判断してW₁とW₂を増やす方向か減らす方向か判断しなければいけないわけですが、この判断を勾配降下法という仕組みで行っています。

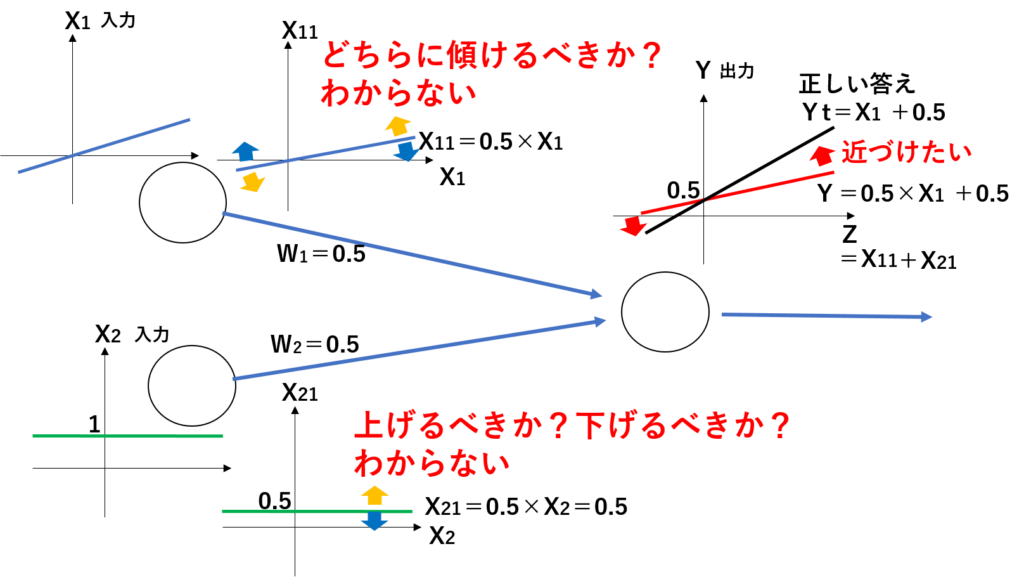
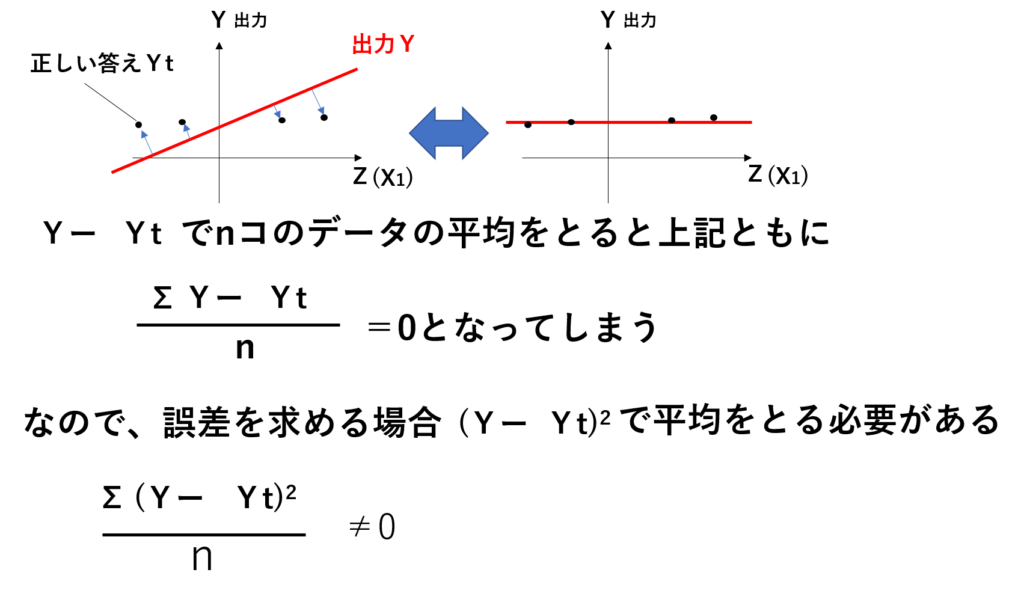
まず、誤差を判断する方法ですが、各出力Yと正しい答えYtとの差を求めて平均化するのではなく、差を累乗し(Y－Yt )²、平均化して求めます(二乗平均誤差)。そうすることで以下の誤差の違いを求めることができるからです。

では、〇番目の誤差である(Y－Yt )²を求めてみます。YはW₁とW₂を変数に持った関数であることがわかります。

これを、それぞれW₁とW₂のグラフにし、極値(最下点)を求めることで、〇番目の誤差をなくすためのW₁とW₂が求まります。

例えばこれが、2番目に読み込まれた入力X₁＝2とX₂＝1に対する出力Yの誤差だったとします。

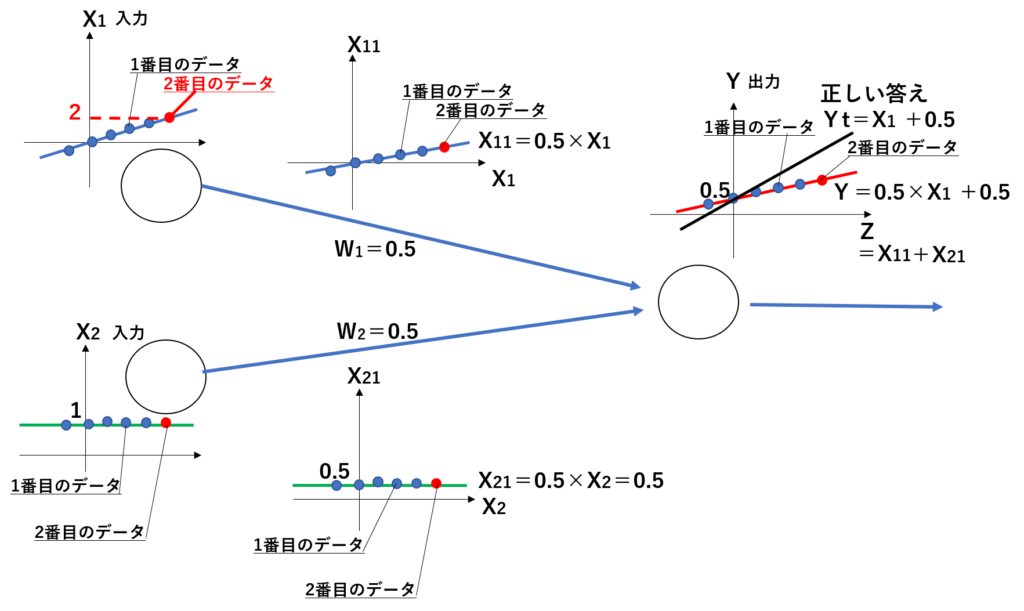
上記の(Y－Yt )²のグラフにX₁＝2とX₂＝1、変数としない方のW₁またはW₂を代入し計算します。これによって、人がこのグラフを見れば、W₁＝1にするか、または、W₂＝1.5にすることで、2番目のデータの誤差を0にできることがわかります。両方の数字をW₁＝1、W₂＝1.5に変えては、誤差が0にはならないため、この値は、W₁、W₂を変化させる方向を示す目標値となります。なので、W₁は0.5⇒1へ向けて、W₂は0.5⇒1.5へ向けて、ともに増やす方向に変化させてゆけばよいとわかります。

ですが、機械学習では、グラフの判断ができないため、先ほどのW₁、W₂を変化させる方向を、(Y－Yt )²を微分した値（(Y－Yt )²グラフの接線の傾き）で判断しています。以下のように(Y－Yt )²を微分し、現在のW₁もしくはW₂の値を入れると、それぞれ、(Y－Yt )²グラフ上での今の接線の傾きが求められます。

この(Y－Yt )²を微分した値が0になれば(Y－Yt )²グラフ上の最下点(目標値)となるわけです。W₁、W₂の微分値(傾き)ともに－2なので、目標値―現在値＝0－（－2）＝2（＞0）で、0に近づけるため、W₁、W₂は、増やせばよいとわかるわけです。

この結果をもとに、各データが読み込まれるたび、W₁、W₂を変化させてゆきます。（たいていは、複数のデータの結果をまとめて、平均化し変化させます。）

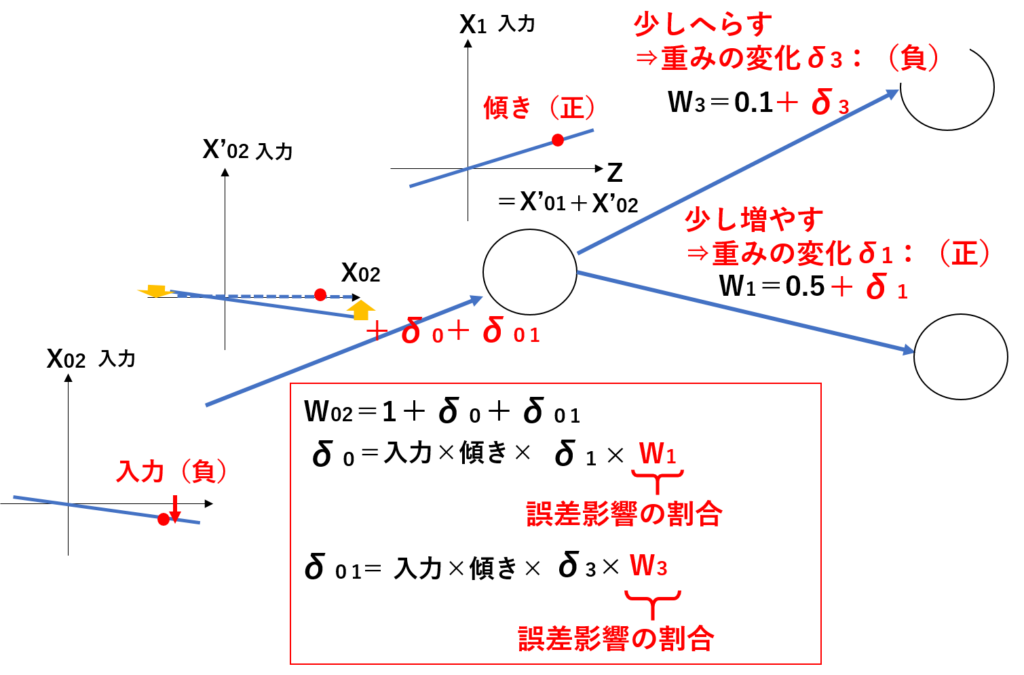
ここまでは、出力に最も近い入力の重みW₁とW₂の変化のプロセスを解説してきました。ここからは、以下のように先ほどの入力X₁が入力X₀₁と入力X₀₂からきている場合、入力X₀₁と入力X₀₂の重みW₀₁とW₀₂は、どのように判断されるかについて説明します。

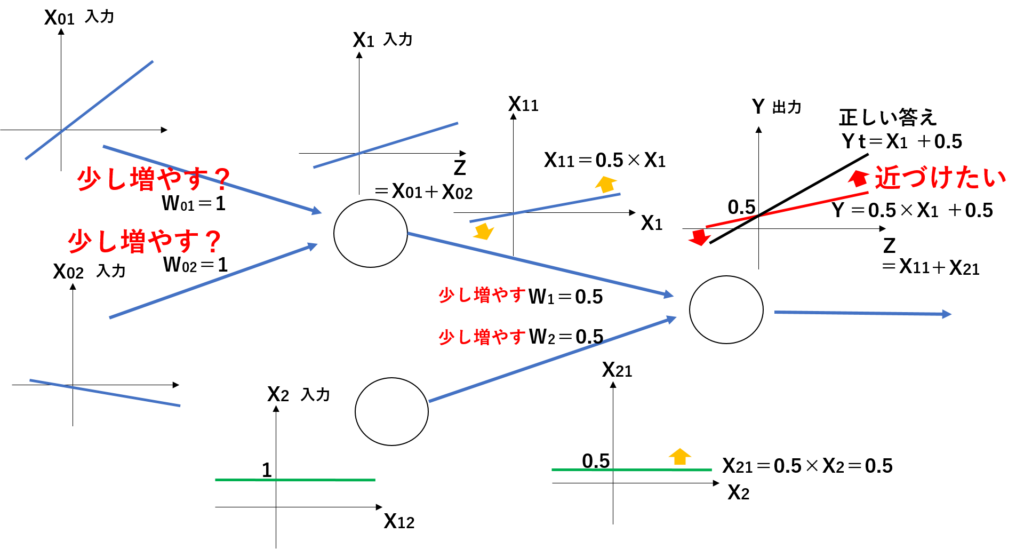
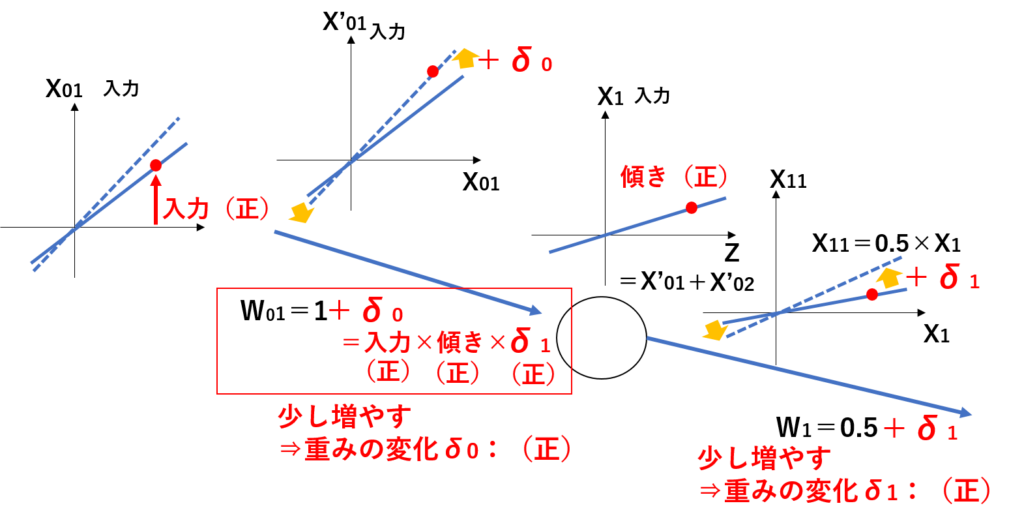
上記の図のうち、W₀₁は、「入力値X₀₁」、「入力値X₀₁とX₀₂に対するX₁の傾き」、先ほどの「W₁の重みの変化させる量」これらをかけ合わせることで、増減を判断させています。

W₀₂についても同様です。「入力値X₀₂」、「入力値X₀₁とX₀₂に対するX₁の傾き」、先ほどの「W₁の重みの変化させる量」これらをかけ合わせることで、増減を判断させています。

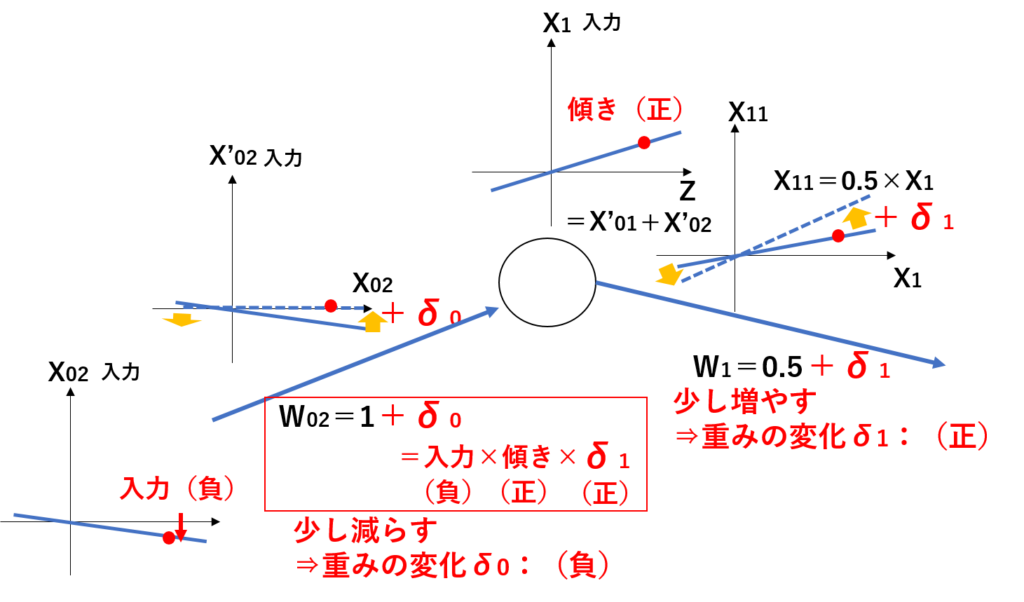
では、以下のようにX1からの入力が二つのニューロンに行っていた場合はどうなるかです。これはX₁からの入力が出力側へ与える影響の大きい方にX₀₂の変化を合わせる必要があります。そこで、先ほどのδ₀の式に、さらに重みW₁を掛けることでX₁からの入力が出力側へ与える誤差影響の割合を反映させてあげます。この計算式を用いた仕組みを、誤差逆伝搬法と呼んでいます。このδの計算を同じようにX₁の出力される枝の数だけ行い、すべてのδを足したものをW₀₂に加えることで、出力側の誤差が入力側に適切な割合で反映されていきます。