ディープランニング(深層学習)は、大きく分けて3つの種類があります。①答え(教師データ)を決めて行う学習、②答え(教師データ)を決めないで行う学習、③強化学習(自ら答えを作り出す学習)
1回目と2回目は、①答え(教師データ)を決めて行う学習の仕組みについて取り上げます。この学習の仕組みは、「回帰分析・分類分析」の2つの分析手法を使用して行われています。
1回目は回帰分析を利用した広く産業界で普及しようとしているIOTによる数値予測の手法を、簡単な例を挙げて紹介したいと思います。
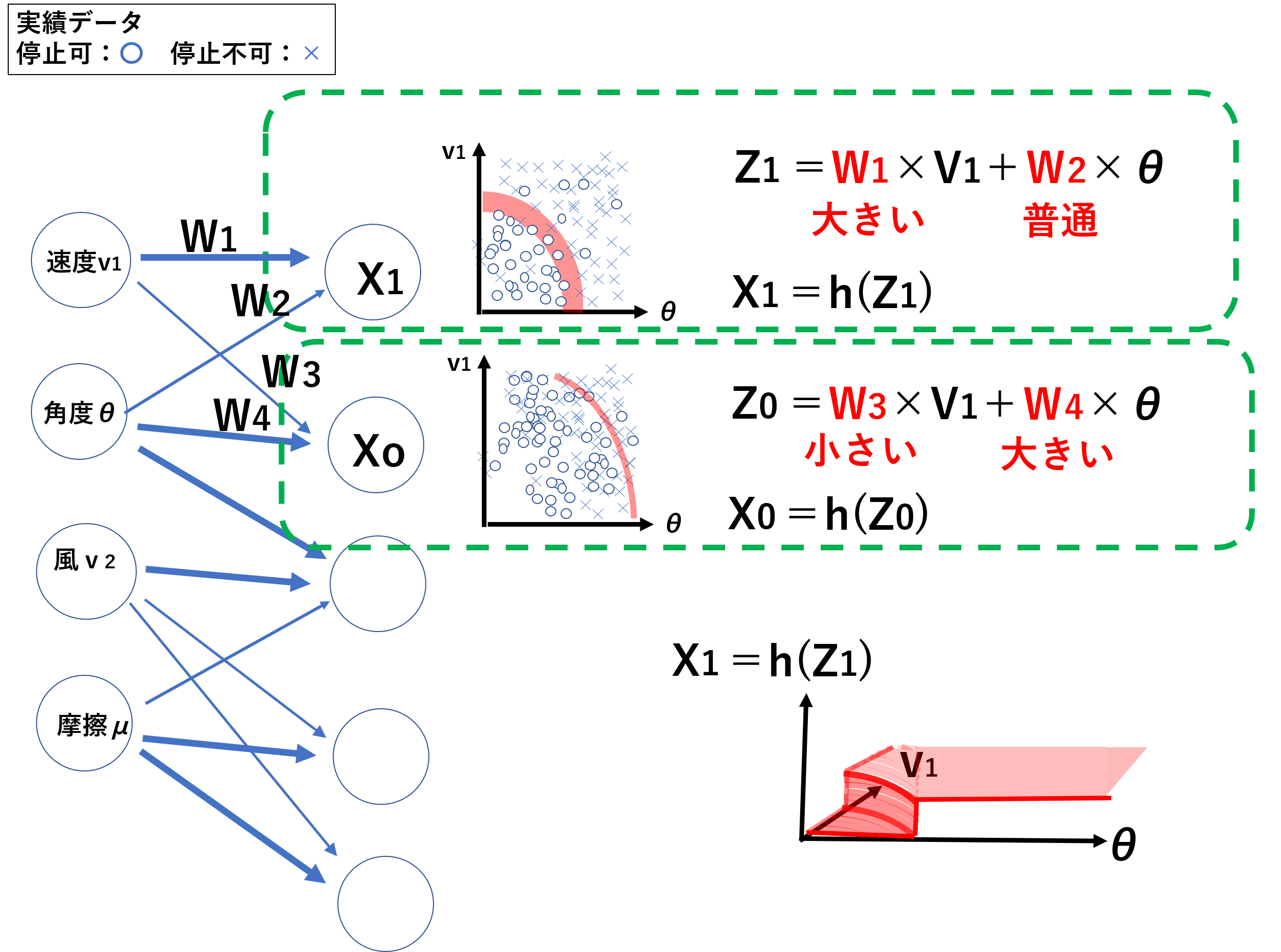
以下のように抵抗に電圧を印加したときの電流の値を求めるとします。電流の値を決める要素は「電圧」と「抵抗の温度」です。
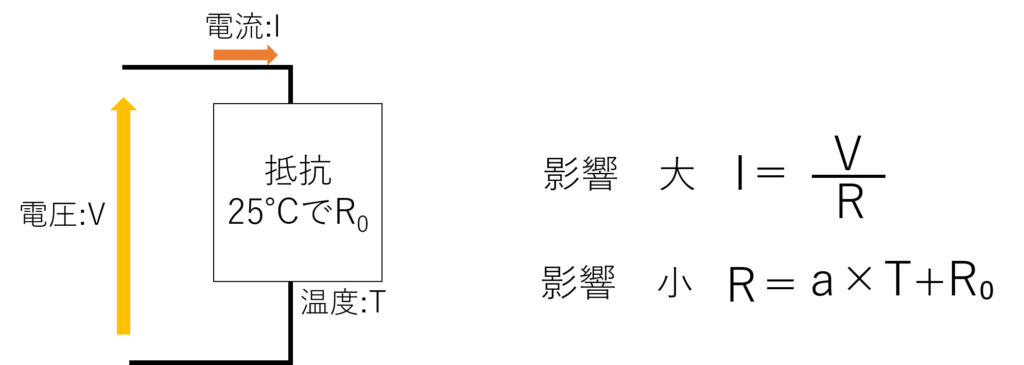
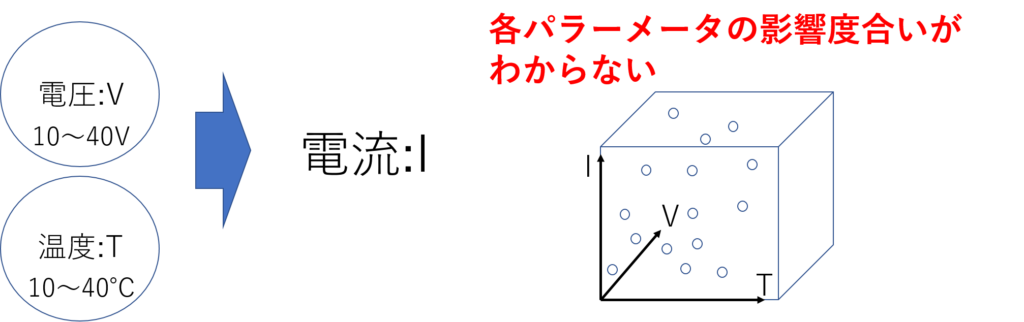
ディープラーニングを行う上で一般的に入力される数値(説明変数)のパラメータは、求める答えに対して、その影響度合いがわかりません。今回についても、機械では単位を認識しているわけではないので、10~40で入力される数値は、電圧が「mV」なのか「V」なのか、温度が×10℃なのか℃なのか、見分けがつかないため、電流に与える影響がわかりません。
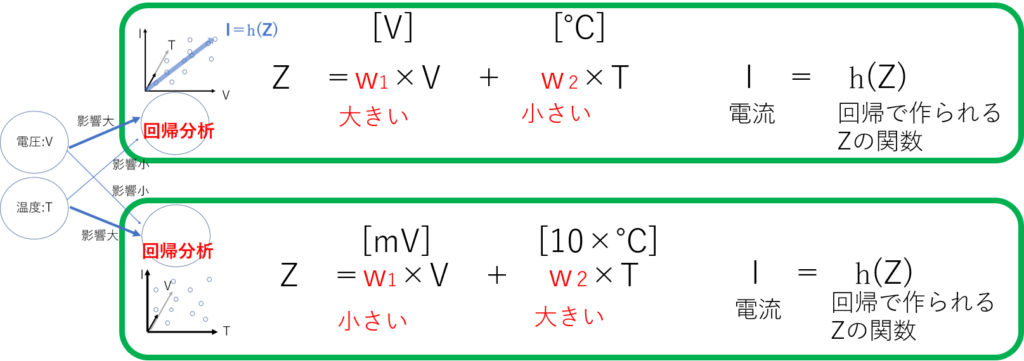
そこで各パラメータの影響度合いを分けて回帰分析を行います。一方は、電圧レンジを「V」・温度レンジを「℃」として、もう一方は、電圧レンジ「mV」・温度レンジ「10×℃」といった具合にです。こうすることで、電流と電圧、電流と温度のグラフが作成されます。(実際は影響の割合を変えた回帰分析の結果がいくつもつくられます。)

次に2つ(本当は複数)の回帰分析の結果から答えとなるデータに近い方の影響を出力に近づけることで、答えの近い回帰分析の結果を見つけだします。

ここまでの計算は、回帰分析・出力前の判別とも同じ以下の式で行われています。

回帰分析の電圧Vと温度Tの影響比率を変更するのは次のようなW係数の割合の変更になります。
出力前の判別は、電流と電圧の回帰分析結果がI21、電流と温度の回帰分析結果がI22なら、次のようにW係数が変更されてゆきます。(このWの係数を変えてゆく仕組みは勾配降下法とういう仕組みを使っています。この計算の仕組みについては3回目で紹介します。)
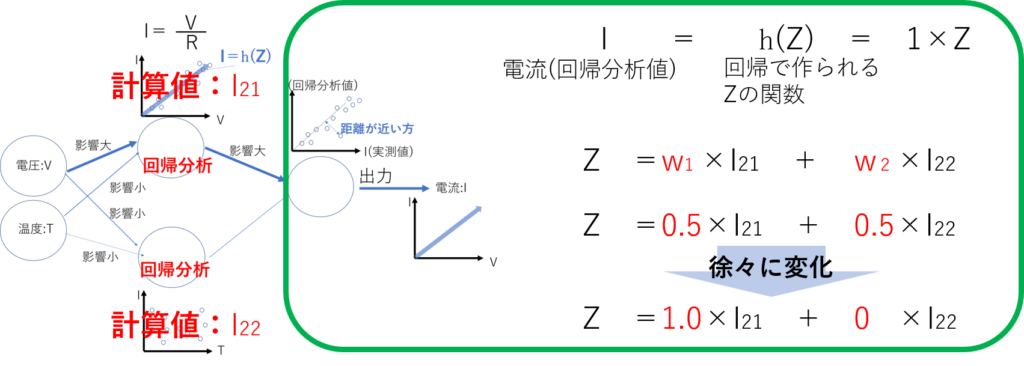
出力前の判別でわかると思いますが、データを繰り返し読み込むことによってWの比重を変化させてゆき、片側のWを最終的に0にする必要があるため、大量のデータが必要になります。
しかし、ディープラーニング(深層学習)のメリットは、ここからさらに一歩踏み込んで、温度の影響についても見つけ出します。最も影響のあるパラメータとの関連を見つけた後、別のパラメータとの関連がないか、さらに複数のパターンの回帰分析を行い、より実測値に近い値を探し出そうとします。データが蓄積されるにしたがって、同じ電圧値における電流が温度と回帰分析されることで、電圧と電流から算出される回帰分析の結果より、正確な数値を得られることを見つけ出すことができます。これが、隠れ層を見つけ出すといわれている仕組みです。

ディープラーニングで扱われるニューラルネットワークの個々のニューロン間は線形の関数しか扱うことができません。つまり、上記の変数である温度と電圧が除算(もしくは乗算)の関係となる相関性を扱うことができないため、ディープラーニングでは以下のように、温度に対していくつかニューロンの線形を足し合わせることで曲線となる相関式を作り出しています。なので、もし温度が決まった範囲のデータで学習していて、学習データと、とてつもなくかけ離れた温度の時の答えをディープラーニングで予想したとした場合、まったく答えとかけ離れた予測結果となってしまいます

次回は分類分析がどのように行われるかについて紹介します。

コメント